Исследование вопросов устойчивости стальных вертикальных цилиндрических резервуаров

/Егоров Е.А., к.т.н., доц., Кустовский А.А., асс. (ПГАСиА, Украина), Набокова И.И. к.т.н., доц./.

Рассматривается влияние несовершенств геометрической формы на устойчивость стальных вертикальных цилиндрических резервуаров, а также устойчивость этих сооружений при ветровой нагрузке. Приводятся результаты проведенных исследований, даются рекомендации по использованию их в инженерной практике.

 (Ключевые слова: вертикальные резервуары, геометрические несовершенства, ветровая нагрузка, потеря устойчивости, деформативность)

 В практике эксплуатации стальных вертикальных цилиндрических резервуаров - наиболее распространенных нефтехранилищ наземного типа, случаи ярко выраженной потери устойчивости практически не имеют места, если не считать аварий, связанных с грубыми нарушениями режимов эксплуатации. По-видимому, именно этим объясняется тот факт, что в отечественной литературе сравнительно мало места уделяется проблеме устойчивости упомянутых сооружений. То же относится и к нормативным документам, касающимся контроля технического состояния резервуаров, находящихся в эксплуатации [1-3].

Вместе с тем с позиций общих представлений теории оболочек проблема устойчивости должна быть и на самом деле является для резервуаров весьма актуальной, поскольку, с одной стороны, имеется целый комплекс сжимающих нагрузок (собственный вес конструкций, ветер, снег, вакуум), с другой стороны, основной конструктивный элемент резервуаров рассматриваемого вида - цилиндрическая стенка - представляет собой очень тонкостенную, а значит и малоустойчивую, оболочку, имеющую, к тому же, многочисленные начальные несовершенства геометрии, что также должно было бы снижать общую ее устойчивость. Нужно также иметь в виду и целый ряд других обстоятельств, которые заставляют постоянно держать под контролем и совершенствовать теоретическую базу оценки устойчивости рассматриваемых сооружений. К ним относятся полный и необратимый выход из строя резервуара после потери общей устойчивости, а также постоянно развивающиеся процессы коррозии, приводящие к уменьшению толщины поясов цилиндрической стенки. Все это заставляет либо выискивать сугубо теоретическим путем имеющиеся резервы, либо принимать какие-то практические, в большинстве своем дорогостоящие, меры в отношении обеспечения устойчивости.

Нами рассматривались и исследовались теоретические аспекты проблемы устойчивости, направленные, однако, на решение практических инженерных задач, в частности, задач диагностики, когда расчетные оценки должны быть максимально приближены к конкретным параметрам диагностируемых объектов.

2. ОЦЕНКА УСТОЙЧИВОСТИ С УЧЕТОМ ИМЕЮЩИХСЯ НЕСОВЕРШЕНСТВ ГЕОМЕТРИЧЕСКОЙ ФОРМЫ

 Исследования, посвященные влиянию несовершенств геометрии на устойчивость тонкостенных оболочек, являются одной из актуальнейших и сложнейших проблем теории устойчивости оболочек и имеют более чем вековую историю. Получено огромное количество результатов, разработано много различных алгоритмов как на основе аналитических, так и численных методов. Вместе с тем применение указанных наработок для оценки устойчивости какого-либо конкретного строительного объекта в виде тонкостенной оболочки сопряжено с целым рядом непреодолимых трудностей из-за большого количества факторов, роль которых в рассматриваемых задачах остается неопределенной. К таким сооружениям относятся и стальные вертикальные цилиндрические резервуары. Большие габариты, высокая тонкостенность, неизбежные начальные несовершенства, в несколько раз превышающие толщину стенки, а также наличие обширного поля сварочных напряжений, по существу, исключают возможность строгого решения рассматриваемой проблемы. В связи с этим в данном случае расчетные оценки строились на базе активного применения асимптотических методов.

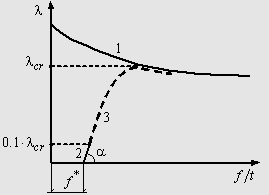
Использовался алгоритм, предложенный в [4], и состоящий в следующем. Для оболочки идеально правильной формы с заданными параметрами геометрии (радиус , толщина , высота цилиндрической стенки резервуара) строится кривая 1 закритического (за точкой потери устойчивости) деформирования, см. рис. 1. Затем для такой же оболочки, но уже с действительной геометрией, т.е. с наличием всех имеющихся дефектов геометрии, строится начальный участок 2 кривой деформирования, который затем с помощью асимптотической аппроксимации сопрягается (участок 3) с кривой 1. Предельная точка участка 3 рассматривается в качестве расчетной оценки критической или предельной (в данном случае это не имеет значения) величины внешнего давления.

Рис. 1. Схема определения предельного внешнего давления.

Все построения и исследовательская часть этого раздела выполнялись с использованием следующих безразмерных параметров:

                                                                                                     (1)

где - величина внешнего давления; - значение критической нагрузки (внешнего давления) для идеально правильной оболочки; - начальная (до приложения нагрузки) величина прогиба (отклонения от поверхности правильного цилиндра) геометрических несовершенств.

Надежность применения такого алгоритма обеспечивается тем, что кривая 1 строится для оболочки, теряющей устойчивость по одной локальной вмятине, и, согласно [5], в таком случае ее можно считать нижней из всех возможных кривых равновесных состояний оболочки с заданными параметрами.

Основная задача приложения рассмотренного выше алгоритма к стальным резервуарам сводилась к построению начального участка деформирования их цилиндрической стенки. Для получения обобщенных оценок устойчивости такой участок строился с учетом характерных для резервуаров несовершенств геометрии, которые определялись на основе многочисленных натурных обмеров геометрии резервуаров различных объемов, находящихся в эксплуатации. В задачах диагностики такой участок строится с учетом действительной геометрии рассматриваемого резервуара.

Дефекты геометрии стальных резервуаров неоднократно рассматривались и анализировались в технической литературе [6, 7]. Однако обычно они представлялись как отклонения образующих от вертикали и в таком виде они не могли использоваться в расчетных оценках. Поэтому, следуя [8],  в данной работе действительная геометрия представлялась в виде отклонений кольцевых сечений поверхности цилиндрической стенки от кольцевых сечений срединной поверхности правильного цилиндра (такие отклонения определяются по тем же отклонениям образующих, но формируются в сверстки по кольцевым горизонтальным сечениям). Аналитически отклонения поверхности цилиндрической стенки резервуара от правильного цилиндра представлялись в виде рядов Фурье по ряду горизонтальных сечений:

…    …    …   …   …   …   …   …  …;

;                                                                                       (2)

где - коэффициенты, определяемые гармоническим анализом результатов натурных обмеров отклонений поверхности цилиндрической стенки от поверхности правильного цилиндра; - порядковый номер (количество окружных волн) той или иной гармоники, являющейся одной из составляющих действительной геометрии цилиндрической стенки;  - угловая координата.

Как показывает гармонический анализ, отклонения поверхности стенки стальных резервуаров от формы правильного цилиндра описываются гармониками 2-8 порядка и имеют амплитуды в пределах =(1.5-10.0), причем с увеличением порядка гармоники значения прогибов уменьшаются. Число волн собственной формы потери устойчивости стенки резервуаров находится в пределах =11-15. Т.е., как правило, отклонения формы, имеющие большие прогибы, далеки от резонансных.

Деформативность цилиндрической стенки определялась и исследовалась по отдельным ее участкам, выделяемым горизонтальными сечениями так, что по высоте каждого отдельного участка амплитуды отклонений могли считаться одинаковыми. Такие участки рассматривались как отдельные тонкостенные гибкие кольца с начальными прогибами (отклонения в виде гофр вертикального направления). Расчетный участок деформирования 2, см. рис. 1, строился для нагрузки  по самому деформативному участку цилиндрической стенки с использованием известных аналитических зависимостей линейного деформирования. Это позволяет существенно упростить решение с однозначным обеспечением некоторого запаса.

В итоге получено, что во многих случаях проектное значение критического напряжения в кольцевом направлении, которое определяется в проектных нормах по формуле:

,                                                                                                 (3)

в действительности оказывается в 1.15-1.30 раза больше. Вместе с тем в отдельных случаях оно может быть и меньше проектного значения.

Для применения полученных результатов в инженерной практике могут быть использованы графики, приведенные в [8].

3. УСТОЙЧИВОСТЬ РЕЗЕРВУАРОВ ПРИ ВЕТРОВОЙ НАГРУЗКЕ

 Исследования устойчивости при действии ветровой нагрузки проводились, опять-таки, с целью получения более дифференцированных расчетных оценок в каждом конкретном случае. Основная проблема состоит здесь в том, что в инженерных методиках действительное распределение ветровой нагрузки заменяется эквивалентным вакуумом, значение которого определяется по формуле:

,                                                                                                                           (4)

где  - максимальная величина активной части ветровой нагрузки.

При этом коэффициент преобразования  во всех случаях, независимо от параметров резервуаров и действительного распределения ветровой нагрузки, принимается равным 0.5.

С физической точки зрения замена ветрового давления эквивалентным равномерным внешним давлением должна осуществляться из условия обеспечения равноустойчивости при указанных воздействиях. Т.е., коэффициент  в (4) должен определяться соотношением:

,                                                                                                                      (5)

здесь  - критическое равномерное внешнее давление;

 - параметр критического ветрового давления.

При этом представляется не совсем правомерным считать  константой, поскольку, во-первых, на основе теоретических представлений должна существовать зависимость параметра критической ветровой нагрузки от того, в какой степени ширина зоны сжатия цилиндрической стенки ветровой нагрузкой резонирует с длиной волны собственной формы потери устойчивости, во-вторых, приведение любого распределения к равномерному безусловно должно зависеть от конкретного вида этого распределения, а характер ветрового давления в каждом конкретном случае зависит от целого ряда факторов и может быть существенно различным, см., например, [9].

В Еврокоде [10] значения  не являются константой и определяются по формуле:

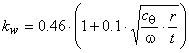,                                                                                                  (6)

где  - коэффициент, зависящий от условий закрепления краев цилиндрической стенки;

 - безразмерный параметр геометрии оболочки (цилиндрической стенки).

В (6)  определяются в зависимости от основных параметров цилиндрической оболочки, однако, по-прежнему, никак не связываются с конкретным законом распределения ветровой нагрузки, т.е., они определены для какого-то фиксированного распределения, заложенного в нормах проектирования.

Учитывая указанные выше обстоятельства, была поставлена задача исследовать особенности поведения цилиндрической стенки стального вертикального цилиндрического резервуара при действии фактического (без приведения к равномерному) давления ветрового типа, которое в принципе может изменяться по любому характерному для ветровой нагрузки закону. Исследования проводились по результатам решения линейной (задача бифуркации) и нелинейной (задача определения предельной нагрузки) задач устойчивости для оболочек, параметры которых соответствовали диапазону параметров типовых решений стальных вертикальных цилиндрических резервуаров: 1500, 3000; . Решение осуществлялось с использованием программного комплекса «Лира 9.2». В данной статье рассматриваются некоторые результаты, полученные только для ветрового давления, распределение которого принято согласно действующим строительным нормам [11], см. рис. 3.

В табл. 1 приведены значения критических  (линейное решение) и предельных  (нелинейное решение)

значений параметра ветрового давления, полученных при шарнирном и жестком закреплениях краев оболочки.

Таблица 1 – Значения критических параметров ветрового давления ( и ), кПа, полученных из линейного и нелинейного решений

		Шарнир		Заделка
1500	1000	3,20	3,18	4,38	4,57
	2000	2,26	2,24	3,20	3,24
	3000	1,94	1,86	2,65	2,66
3000	1000	0.75	0,78	1,02	1,10
	2000	0.5	0,55	0,70	0,81
	3000	0.44	0,45	0,62	0,65

Сравнение результатов линейного и нелинейного решений показывает, что различия критических и предельных  значений ветрового давления не превышают 5-10%. При этом, как видно из табл. 1, более низким может оказаться как , так и . Отсюда следует, что в общем случае для получения надежной оценки устойчивости

необходимо проведение линейного и нелинейного анализа.

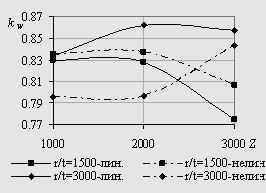
Приведенные на рис. 2 графики показывают, что  существенно зависит от основных геометрических параметров цилиндрической стенки резервуаров и может изменяться от 0,77 до 0,92. По (6) для таких же оболочек значения  получаются равными от 0.65 до 1.0.

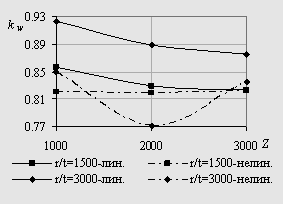
Рис. 2. Значения коэффициента , полученные из линейного и нелинейного решений:

а) шарнирное опирание; б) жесткая заделка.

а)

б)

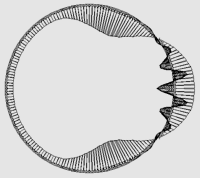
Анализ результатов показывает, что изменяются не только значения , но и форма деформирования цилиндрической стенки. На рис. 3 показано, что в центре зоны активного ветрового давления (наветренная сторона) в одних случаях может образовываться вмятина, в других – выпучина. Т.е., изменение масштабности сопровождается в данном случае не только количественными, но и качественными изменениями в поведении оболочек.

Рис. 3. Формы потери устойчивости оболочек с r/t = 3000: a) Z=2000; б) Z=3000.

а)                                                                б)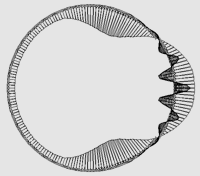

Заслуживает внимания и характерный вид кривых деформирования в координатах «нагрузка-прогиб». На рис. 4 показаны такие кривые, полученные нелинейным решением.

Рис. 4. Кривые деформирования оболочки с  параметрами  r/t =1500, Z=1000.

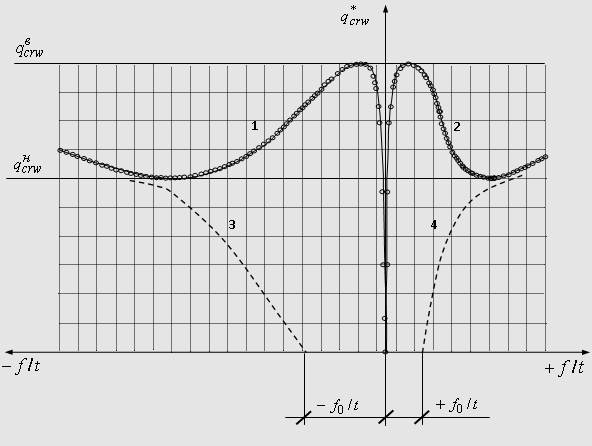
Кривые 1, 2 на рис. 4 являются кривыми деформирования оболочки правильной формы до и после достижения верхней предельной точки. Кривая 1 показывает развитие наибольшей образовавшейся вмятины, а кривая 2 – то же, выпучины. Для всех исследованных параметров цилиндрической стенки резервуаров на кривых закритического деформирования отчетливо прослеживается верхняя  и нижняя  предельные точки, соответствующие верхней  и нижней  критическим нагрузкам, при этом во всех случаях за нижней предельной точкой имеет место возрастающий участок кривой деформирования. Значения прогибов при достижении нижней предельной точки изменяются в диапазоне , что приблизительно соответствует начальным параметрам отклонений в натурных резервуарах.

Это позволяет сделать вывод о том, что процесс деформирования имеет в целом устойчивый характер (см. рис. 4, кривые 3, 4), а сама по себе ветровая нагрузка не представляет особой опасности для общей потери устойчивости. С другой стороны, возникновение больших прогибов может сопровождаться развитием местных пластических деформаций. Поэтому в инженерных расчетах в качестве предельного значения параметра ветровой нагрузки предлагается принимать . В каждом же конкретном случае решение задач устойчивости в диагностических оценках технического состояния стальных резервуаров требует проведения линейного и нелинейного анализа с учетом рассмотренных в данной статье особенностей геометрии цилиндрической стенки и действующих нагрузок. Такой анализ неоднократно применялся нами по отношению к натурным резервуарам. В большинстве случаев это позволяло выявить имеющиеся резервы устойчивости, а в некоторых случаях это являлось серьезной аргументацией для проведения работ по усилению. На рис. 5 показано усиление резервуара объемом 10 тыс. м³, выполненное по нашим рекомендациям.

Рис. 5. Усиление резервуара объемом 10 тыс. м³.

4. ЗАКЛЮЧЕНИЕ

 Приближенные, но однозначно обеспечивающие «запас» методы оценки устойчивости стальных вертикальных цилиндрических резервуаров от внешнего давления (вакуум или эквивалентная ветровая нагрузка) позволяют использовать их в инженерной практике и в большинстве случаев на основе учета действительной геометрии (с учетом дефектов и повреждений) выявлять имеющиеся резервы устойчивости цилиндрической стенки резервуаров, находящихся в эксплуатации.

Анализ результатов решения задачи устойчивости стальных вертикальных цилиндрических резервуаров при действии ветровой нагрузки в линейной и нелинейной постановке показывает, что значения коэффициента  существенно зависят от геометрических параметров цилиндрической стенки резервуаров и для принятой в типовых проектах номенклатуры резервуаров находятся в пределах 0.77-0.92.

Нелинейный анализ закритического поведения оболочек позволяет считать, что деформирование цилиндрической стенки резервуаров рассматриваемого вида под действием ветровой нагрузки имеет в целом устойчивый характер. В инженерной практике, учитывая наличие начальных несовершенств геометрической формы, предельно допустимое значение ветровой нагрузки рекомендуется ограничивать нижним критическим значением .

ЛИТЕРАТУРА:

1. Правила технической эксплуатации резервуаров и инструкции по их ремонту. Госкомнефтепродукт СССР, утверждено 26.12.1986 г.

2. Руководство по обследованию и дефектоскопии стальных вертикальных резервуаров (РД-95). Госкомнефтепродукт России. – Астрахань, 1995. –С. 145.

3. Инструкция по техническому надзору, методам ревизии и отбраковке трубчатых печей, резервуаров, сосудов и аппаратов нефтеперерабатывающих и нефтехимических производств.- ИТН-93. – Волгоград, 1995. – С. 189.

4. Евкин  А.Ю. Новый подход к асимптотическому анализу устойчивости и закритического поведения строго выпуклых пологих оболочек: ДИСИ.- Днепропетровск, 1988. - С.17.  Деп. в УкрНИИНТИ 01.07.88, N 1710.

5. Евкин.А.Ю., Красовский В.Л. Закритическое деформирование и оценка устойчивости реальных цилиндрических оболочек при внешнем давлении // Прикладная механика.- 1991.- т.27. - N 3.-С. 76-83.

6. Сафарян М.К., Писанко Н.М. Исследование геометрической формы стальных вертикальных цилиндрических резервуаров // Сб. науч. трудов / ВНИИСтройнефть.- 1957.- Вып.IX. – С.14-23.

7. Сафарян М. К. Металлические резервуары и газгольдеры. - М.: Недра, 1987.-С. 200.

8. Егоров Е.А. Исследования и методы расчетной оценки прочности, устойчивости и остаточного ресурса стальных резервуаров, находящихся  в эксплуатации.-Дніпропетровськ: Навчальна книга, 2002. – 95с.

9. Кінаш Р.І., Копилов О.Є. Аеродинамічні дослідження тандему з двох колових циліндрів // Теорія і практика будівництва: Вісник НУ „ЛП”.-Львів: НУ „ЛП”.- 2002.-№441.-С.85-94.

10. CEN/TC 250/SC3/PT4 Eurocode 3: Design of steel structures. Part 1-6: General Rules: Supplementary Rules for Shell Structures. – Brussels: Centr. Secr., 1999. – 83 p.

11. СНиП 2.01.07-85 Нагрузки и воздействия / Госстрой СССР. – М.: ЦИТП Госстроя СССР, 1987. – 36 с.

12. СНиП II-23-81* Стальные конструкции. / Госстрой СССР. – М.: ЦИТП Госстроя СССР, 1990. – 96 с.