Линейный и нелинейный анализ устойчивости стальных вертикальных цилиндрических резервуаров при ветровой нагрузке
/Егоров Е.А., к.т.н., доц., Федоряка Ю.В. аспирант (ПГАСиА, Украина)/.
Актуальность проблемы. Проблема устойчивости стальных вертикальных цилиндрических резервуаров, используемых для хранения нефтепродуктов, имеет немаловажное значение, поскольку при полной потере устойчивости резервуар становится неработоспособным, и конструкции его практически не подлежат восстановлению, что влечет за собой значительный материальный ущерб. Проблема устойчивости указанных сооружений при ветровой нагрузке особенно актуальна, так как установлено, что для резервуаров, эксплуатируемых в климатических условиях Украины, сжимающие напряжения, обусловленные ветровой нагрузкой, имеют определяющее значение.
Постановка задачи. В действующих нормах проектирования [2] при оценке устойчивости стальных резервуаров учет ветровой нагрузки осуществляется весьма приближенно: неравномерно распределенное по периметру цилиндрической стенки резервуара ветровое давление приводится к равномерному внешнему давлению (эквивалентному вакууму), значение которого определяется по формуле:
![]() ,
(1)
,
(1)
где
![]() - ордината эпюры ветрового давления при
- ордината эпюры ветрового давления при
![]() (
(![]() - центральный угол).
- центральный угол).
При этом коэффициент
![]() во всех случаях принимается равным 0,5. В европейских
нормах проектирования
[4]
ветровая нагрузка также заменяется равномерным давлением, но коэффициент
приведения при этом определяется в зависимости от основных геометрических
параметров цилиндрической стенки резервуара:
во всех случаях принимается равным 0,5. В европейских
нормах проектирования
[4]
ветровая нагрузка также заменяется равномерным давлением, но коэффициент
приведения при этом определяется в зависимости от основных геометрических
параметров цилиндрической стенки резервуара:
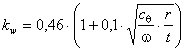 , (2)
, (2)
где![]() - коэффициент, зависящий от условий закрепления торцов
цилиндрической стенки;
- коэффициент, зависящий от условий закрепления торцов
цилиндрической стенки;
![]() - параметр геометрии цилиндрической стенки резервуара;
- параметр геометрии цилиндрической стенки резервуара;
![]() - соответственно, длина, радиус и толщина цилиндрической
стенки.
- соответственно, длина, радиус и толщина цилиндрической
стенки.
В (2) значения
коэффициента
![]() определяются в зависимости от основных геометрических
параметров резервуара, но сам по себе вид формулы (2) записан для какого-то
конкретного закона распределения ветровой нагрузки. В отношении этого можно
отметить, что, согласно известным положениям теории устойчивости оболочек,
коэффициент
определяются в зависимости от основных геометрических
параметров резервуара, но сам по себе вид формулы (2) записан для какого-то
конкретного закона распределения ветровой нагрузки. В отношении этого можно
отметить, что, согласно известным положениям теории устойчивости оболочек,
коэффициент
![]() должен
зависеть не только от
параметров цилиндрической стенки, но и от закона распределения давления,
который в практике эксплуатации стальных резервуаров может изменяться в
зависимости от рельефа местности, взаимного расположения резервуаров, а
также в сочетаниях с эксплуатационным вакуумом.
должен
зависеть не только от
параметров цилиндрической стенки, но и от закона распределения давления,
который в практике эксплуатации стальных резервуаров может изменяться в
зависимости от рельефа местности, взаимного расположения резервуаров, а
также в сочетаниях с эксплуатационным вакуумом.
Учитывая выше изложенное, была поставлена задача исследовать особенности поведения цилиндрической стенки стального вертикального резервуара при действии ветровой нагрузки с учетом ее фактического распределения.
Содержание исследований.
Исследования проводились численным методом (МКЭ) с применением программных
комплексов «ЛИРА 9.2» и «Cosmos M 2.6».
Рассматривались цилиндрические оболочки постоянной толщины, геометрические
параметры которых соответствовали основным геометрическим параметрам
применяемых в настоящее время типовых решений вертикальных цилиндрических
резервуаров:
![]() ;
;
![]() . Конечно-элементные (КЭ) модели цилиндрических оболочек
строились в трехмерной постановке с применением прямоугольных конечных
элементов оболочечного типа, общее число которых составило около 7000 шт.,
количество неизвестных линейных и угловых перемещений – до 36000. Указанные
прямоугольные конечные элементы имеют в каждом узле по 6 степеней свободы (3
линейных и 3 угловых перемещения), и учитывают мембранные, изгибные и
касательные усилия. Операции выбора типа конечного элемента, дискретизации
КЭ моделей оболочек и приложения нагрузки были стандартными и здесь детально
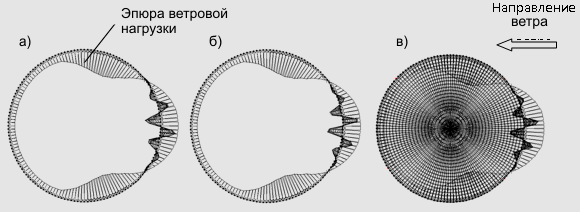
не описываются. Вид нагрузки приведен на рис. 1. При назначении граничных
условий (ГУ) были рассмотрены варианты с шарнирными и жесткими закреплениями
торцов оболочки, см. варианты №№ 1-2 в табл. 1, а также два варианта ГУ с
жестким плоским диском (№№ 3-4, табл. 1), установленным по верху оболочки и
моделирующим наличие стационарной кровли.
. Конечно-элементные (КЭ) модели цилиндрических оболочек
строились в трехмерной постановке с применением прямоугольных конечных
элементов оболочечного типа, общее число которых составило около 7000 шт.,
количество неизвестных линейных и угловых перемещений – до 36000. Указанные
прямоугольные конечные элементы имеют в каждом узле по 6 степеней свободы (3
линейных и 3 угловых перемещения), и учитывают мембранные, изгибные и
касательные усилия. Операции выбора типа конечного элемента, дискретизации
КЭ моделей оболочек и приложения нагрузки были стандартными и здесь детально
не описываются. Вид нагрузки приведен на рис. 1. При назначении граничных
условий (ГУ) были рассмотрены варианты с шарнирными и жесткими закреплениями
торцов оболочки, см. варианты №№ 1-2 в табл. 1, а также два варианта ГУ с
жестким плоским диском (№№ 3-4, табл. 1), установленным по верху оболочки и
моделирующим наличие стационарной кровли.
Таблица 1
Условия закрепления краев оболочек|
№ вар-та |
Наименование | Координата | Граничные условия |
| 1 | Шарнирное опирание | z=0, l | v=0; w=0 |
| 2 | Жесткая заделка | z=0, l | u=0; v=0; w=0; du/dz=0; dv/dy=0; dw/dx=0 |
| 3 | Жесткий диск + шарнир | z=0 | v=0; w=0 |
| z=l | жесткий диск | ||
| 4 | Жесткий диск + заделка | z=0 | u=0; v=0; w=0; du/dz=0; dv/dy=0; dw/dx=0 |
| z=l | жесткий диск |
Обозначения, принятые в табл. 1: u, v, w, – соответственно, меридиональное, кольцевое и радиальное линейные перемещения; du/dz, dv/dy, dw/dx – то же, угловые перемещения.
Исследования выполнялись
в три этапа. На первом этапе выполнялся анализ напряженно-деформированного
состояния (НДС) цилиндрической оболочки при действии ветровой нагрузки.
Задача данного этапа состояла в дополнительном апробировании работы
программных комплексов и принятых принципов формирования конечно-элементных
моделей резервуара, а также уточнялись некоторые особенности, косвенным
образом определяющие устойчивость рассматриваемых оболочек. Получено, что,
как и следовало ожидать, рассматриваемые цилиндрические оболочки имеют
большой запас по прочности, и действие
ветровой нагрузки на
цилиндрический резервуар является проблемой устойчивости, а не прочности. Во
всех случаях значения кольцевых напряжений не превышали 12-18 МПа, а
эквивалентных напряжений – 17-20 МПа. Сравнение результатов расчета
оболочек, имеющих классические виды закреплений на торцах (ГУ №№ 1-2), с
консольными оболочками (оболочки с жестким диском-кровлей) показывает, что
различия в величине напряжений являются совершенно несущественными. Это
обусловлено, очевидно, тем, что незначительными являются горизонтальные
перемещения жесткого диска. Так, для оболочки с
![]() ,
,
![]() при ГУ №3 и нагрузке
при ГУ №3 и нагрузке
![]() кПа указанные перемещения составили 0,536 мм (
кПа указанные перемещения составили 0,536 мм (![]() ), а для этой же оболочки при ГУ №4 – 0,392 мм (
), а для этой же оболочки при ГУ №4 – 0,392 мм (![]() ). Моментные составляющие для рассматриваемого
распределения нагрузки оказываются во всех случаях незначительными:
). Моментные составляющие для рассматриваемого
распределения нагрузки оказываются во всех случаях незначительными:
![]() МПа.
МПа.
Как ранее было указано, ветровая нагрузка на цилиндрические резервуары представляет собой неравномерное внешнее давление. В работе [1] отмечено, что при неравномерных нагружениях, характеризующихся сильным докритическим изгибом, применение линейного расчета устойчивости с использованием линейной моментной модели докритического состояния дает существенные погрешности, так как при этом не учитываются большие докритические прогибы, исключаются из рассмотрения нелинейные эффекты качественного характера, например, перестройка докритической формы с увеличением нагрузки. И поэтому в таких случаях необходимо применение нелинейного анализа поведения оболочек. В рассматриваемой задаче моментные составляющие оказываются незначительными (см. выше), однако, на фоне таких же незначительных мембранных усилий их роль в устойчивости заранее предсказать весьма трудно. Поэтому в данном случае важными могут оказаться результаты как линейного решения задачи устойчивости, так и нелинейного анализа деформирования цилиндрической стенки резервуара под воздействием ветровой нагрузки.
На втором этапе выполнялось
решение бифуркационной (линейной) задачи устойчивости, в результате которой
определялся параметр критического ветрового давления
![]() и ассоциируемая с ним форма потери устойчивости оболочки.
Полученные формы потери устойчивости для оболочки с
и ассоциируемая с ним форма потери устойчивости оболочки.
Полученные формы потери устойчивости для оболочки с
![]() ,
,
![]() при вариантах ГУ №№ 1-3 приведены на рис 1.
при вариантах ГУ №№ 1-3 приведены на рис 1.
Рис. 1. Формы потери
устойчивости оболочки с
![]() ,
,
![]() при ГУ:
при ГУ:
а) вариант №1; б) вариант №2; в) вариант №3.
На данном этапе помимо ветровой
нагрузки рассматривалось загружение оболочек равномерным внешним давлением.
Получено, что длины волн форм потери устойчивости оболочек при равномерном
давлении и ветровой нагрузке при одинаковых условиях закрепления весьма
близки. Отношение параметра критической ветровой нагрузки оболочек с жесткой
заделкой
![]() к аналогичному параметру шарнирно опертых оболочек
к аналогичному параметру шарнирно опертых оболочек
![]() составило
составило
![]() . Эти результаты хорошо согласуются с данными,
приведенными в [3],
полученными для
. Эти результаты хорошо согласуются с данными,
приведенными в [3],
полученными для
случая равномерного давления.
На третьем этапе исследований
был выполнен нелинейный анализ деформирования оболочек при ветровой
нагрузке. В результате были определены значения параметра предельной
ветровой нагрузки
![]() , деформированные схемы оболочек, а также зависимости
«нагрузка-перемещение» (в качестве характерного перемещения рассматривалось
радиальное перемещение
, деформированные схемы оболочек, а также зависимости
«нагрузка-перемещение» (в качестве характерного перемещения рассматривалось
радиальное перемещение
![]() ). Значения параметров критической ветровой нагрузки,
полученных из линейного (
). Значения параметров критической ветровой нагрузки,
полученных из линейного (![]() ) и нелинейного (
) и нелинейного (![]() ) анализов, а также значения критического равномерного
давления
) анализов, а также значения критического равномерного
давления
![]() для оболочек с параметрами
для оболочек с параметрами
![]() ,
,
![]() , приведены в табл.2.
, приведены в табл.2.
Таблица 2
Параметры критической
![]() и предельной
и предельной
![]() ветровой нагрузки, критическое равномерное давление
ветровой нагрузки, критическое равномерное давление
![]() , кПа
, кПа
|
r / t |
Вариант ГУ | Z = 1000 | Z = 2000 | Z = 3000 | ||||||
|
|
|
|
|
|
|
|
|
|
||
|
1500 |
№1 | 2,84 | 3,44 | 3,18 | 1,97 | 2,46 | 2,24 | 1,58 | 2,03 | 1,86 |
| №2 | 4,07 | 4,82 | 4,57 | 2,85 | 3,48 | 3,24 | 2,31 | 2,88 | 2,66 | |
| №3 | 3,51 | 4,16 | 3,86 | 2,45 | 3,01 | 2,74 | 1,99 | 2,49 | 2,25 | |
| №4 | 4,15 | 4,85 | 4,57 | 2,89 | 3,50 | 3,24 | 2,40 | 2,89 | 2,67 | |
Получено, что для большинства рассматриваемых оболочек при всех ГУ более низкое значение критической нагрузки дает нелинейный расчет, что подтверждается данными, приведенными в табл. 2.
Анализ деформированных схем оболочек, полученных из нелинейного расчета, показал, что по мере увеличения нагрузки перестроек формы выпучивания оболочек не наблюдается. Отсюда, учитывая положения работы [1], можно сделать вывод о том, что изменяемость ветровой нагрузки невелика. Данный вывод подтверждается и тем, что отклонения значений критических нагрузок, полученных из линейного и нелинейного расчетов, невелики и составляют 5-10%, см. табл. 2. В то же время нужно, очевидно, считать, что для получения надежных значений критической ветровой нагрузки необходимо выполнение как линейного, так и нелинейного анализа.
Получив значения критического ветрового давления, можно определить коэффициент приведения ветровой нагрузки к равномерному давлению по формуле:
![]() ;
(3)
;
(3)
где
![]() - наименьшее из двух значений параметра критической
ветровой нагрузки, определенных линейным и нелинейным расчетом.
- наименьшее из двух значений параметра критической
ветровой нагрузки, определенных линейным и нелинейным расчетом.
Для рассматриваемых оболочек
![]() 0,71?0,99.
Отметим, что по [4]
для рассматриваемых оболочек значения
0,71?0,99.
Отметим, что по [4]
для рассматриваемых оболочек значения
![]() составили:
составили:
![]() 0,652?1,0.
0,652?1,0.
Отдельного рассмотрения
заслуживают графики зависимости «нагрузка-перемещение», получаемые
нелинейным расчетом. На рис. 2 приведен характерный вид кривых
деформирования, полученный для оболочки с
![]() ,
,
![]() при ГУ №1. На обеих кривых четко прослеживаются верхняя и
нижняя предельные точки.
при ГУ №1. На обеих кривых четко прослеживаются верхняя и
нижняя предельные точки.
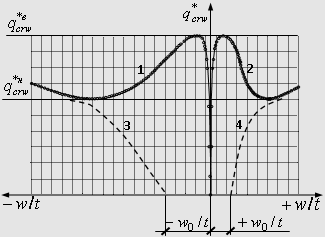
Рис. 2. Кривые деформирования
оболочки с параметрами
![]() ,
,
![]() .
.
Установлено, что в случае
шарнирного опирания соотношение предельных нагрузок в нижней
![]() и верхней
и верхней
![]() предельных точках изменялось в диапазоне
предельных точках изменялось в диапазоне
![]() ; при жесткой заделке это соотношение составило
; при жесткой заделке это соотношение составило
![]() . При этом верхней предельной нагрузке соответствуют
перемещения
. При этом верхней предельной нагрузке соответствуют
перемещения
![]() для всех ГУ, а нижней предельной нагрузке в случае
шарнирного опирания оболочки -
для всех ГУ, а нижней предельной нагрузке в случае
шарнирного опирания оболочки -
![]() , в случае жесткого защемления -
, в случае жесткого защемления -
![]() .
.
Интересно отметить, что
указанные величины радиальных перемещений находятся в диапазоне характерных
начальных отклонений поверхности цилиндрической стенки вертикальных
резервуаров от формы правильного цилиндра. Принимая в учет это
обстоятельство, а также известные асимптотические подходы к оценке
устойчивости несовершенных оболочек
[5],
в инженерных расчетах оценку устойчивости рекомендуется выполнять,
ориентируясь на нижнее значение предельной нагрузки
![]() . На том же рис.2 показаны кривые 3,4 , являющиеся кривыми
деформирования оболочки с начальными несовершенствами, характеризующимися
величиной начального прогиба
. На том же рис.2 показаны кривые 3,4 , являющиеся кривыми
деформирования оболочки с начальными несовершенствами, характеризующимися
величиной начального прогиба
![]() . Как видно из рис. 2, указанные кривые асимптотически
приближаются к нижним предельным точкам деформирования правильных оболочек.
. Как видно из рис. 2, указанные кривые асимптотически
приближаются к нижним предельным точкам деформирования правильных оболочек.
Заключение. Анализ результатов решения задачи устойчивости стальных вертикальных цилиндрических резервуаров при действии ветровой нагрузки в линейной и нелинейной постановках показывает, что значения критических параметров нагрузки ветрового типа и ее предельные значения на кривых нелинейного деформирования весьма близки. Это позволяет сделать вывод о том, что для получения надежной оценки устойчивости рекомендуется проводить линейный и нелинейный анализ устойчивости с учетом особенностей геометрии цилиндрической стенки и характера действующих нагрузок.
При наличии в цилиндрической стенке резервуара начальных несовершенств геометрической формы определение предельного параметра ветровой нагрузки необходимо осуществлять ориентируясь на нижнее предельное значение указанного параметра для правильных оболочек.
В инженерных расчетах
приведение ветрового давления к равномерному можно осуществить, используя
коэффициент приведения
![]() , который для резервуаров рассматриваемого типа в
зависимости от конкретных геометрических параметров принимает значения в
пределах 0.71-0.99.
, который для резервуаров рассматриваемого типа в
зависимости от конкретных геометрических параметров принимает значения в
пределах 0.71-0.99.
ЛИТЕРАТУРА:
[1]. Андреев Л.В., Ободан Н.И., Лебедев А.Г. Устойчивость оболочек при неосесимметричной деформации. – М.: Гл. ред. физ.-мат. лит., 1988. – 207 с.
[2]. ВБН В 2.2-58.2-94. Резервуари вертикальні сталеві для зберігання нафти і нафтопродуктів з тиском насичених парів не вище 93,3 кПа / Державний Комітет України по нафті і газу. – Київ, 1994. – 95 с.
[3]. Григолюк Э.И., Кабанов В.В. Устойчивость оболочек. – М.: Наука, 1978. – 359 с.
[4]. CEN/TC 250/SC3/PT4 Eurocode 3: Design of steel structures. Part 1-6: General Rules: Supplementary Rules for Shell Structures. – Brussels: Centr. Secr., 1999. – 83 p.
[5]. Yegorov Y.A., Ismagulov B.G., Fedoryaka Y.V. Stability Estimate of Vertical Cylinder-Shaped Tanks in service// International Conference on Design, inspection, maintenance and operation of cylindrical steel tanks and pipelines. – Praque, Czech Republic. – October 8 to 10, 2003. – P. 336-341.
LINEAR AND NONLINEAR ANALYSIS OF STABILITY OF STEEL VERTICAL
CYLINDRICAL TANKS AT WIND LOAD
Eugen Yegorov, Julia Fedoryaka
Prydniprovskaya State Academy of Building and Architecture
Behavior features of steel vertical cylindrical oil storage tanks at wind loading are examined. The results of stress-strain state of these structures, and results of linear and nonlinear solving of stability problem are considered. Recommendations for taking wind load into account at tank stability estimate are given.